構造計算地震力について
構造 計算 地震 力について解説していきます。
地震が起きると建物は、たてや横に揺れます。

ただ構造設計に関しては横(水平方向)にゆれた事として
計算していきます。
この地震による水平方向の揺れの大きさ(応力)を計算で求めて、
建物の材料の強度を、横揺れに耐えられるように
材料を選定していく事になります。
地震による水平方向の揺れとは?
地震によって水平方向の揺れると各階(各層)には、
せん断力が発生します。
せん断力とは、物体をゆがめる力です。
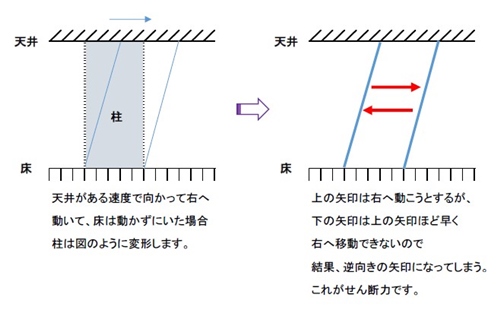
この建物をせん断しようとする力が地震力です。
地震力の公式
地震力を式で書くとこうなります。
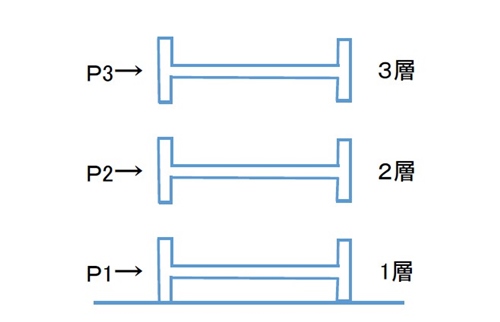
『P 地震力』=k(水平震度)× W(建物重量)
水平震度とは、『標準層せん断力係数 (Co)』の事です。
『標準層せん断力係数』の『層』とはフロアの事で『各階』の事です。
通常、Co=0.2で計算します。
構造計算で地震力をかける位置は?
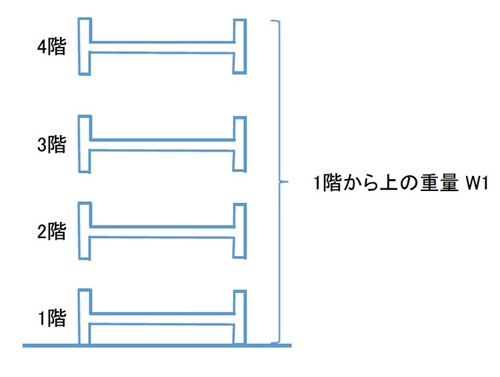
構造計算で地震力をかける位置は、各階の床にかけます。
重さは床に集中しているとして、床に水平の地震力をかけます。
柱や壁は半分にし、上か下の階の床に組み入れます。
地震加速度0.2Gは、様々な計数で補正します。
が、仮に0.2Gで1階のせん断力を計算すると、
0.2×(1層の重さ+2層の重さ+3層の重さ)と言う事になります。
地震加速度0.2Gの補正の仕方
地震加速度0.2Gのを補正するには、『地震層せん断係数』と言うものを使います。
地震層せん断係数はCiという記号を使います。
iは階数を表しています。
地震層せん断係数(Ci)は次の式で求めます。
Ci(i層の地震層せん断力係数)=Z×Rt×Ai×Co
記号の意味は下記の通りです。
Z : 地震地域係数
Rt : 振動特性係数
Ai : 高さ方向の分布係数
Co : 標準せん断力係数
地震地域係数Zとは?
地震地域係数Zとは、過去の地震の統計から定めた地域別の
低減係数です。
低減率が壱番高いのは沖縄県で0.7です。
本州の太平洋側は低減無しの1となります。
振動特性係数とはRtとは?
地震が起きた時、どんな建物でも
同じように揺れるかといえば、そうではないですよね。
タワーマンションのような高層のものは大きくゆっくり揺れるのに対し、
揺れが小さい建物のもあります。
一般的に重いほど大きく揺れ、固いほど小さく揺れます。
この建物特有の揺れ方の違いを、建物の固有周期と言います。
振動特性係数とはRtは、建物の固有周期と、地盤の振動特性に
よって決まる低減係数です。
例えば高さ H (m)での固有周期 (T)は、
RC造りで0.02 S造りや木造で0.03となります。
RCに比べ、S造りや木造は建物自体、柔らかいので周期が長くなります。
この0.02や0.03を建物の高さに掛け、固有周期 (T)を求めます。
RC
固有周期 (T) = 0.02h
S造りや木造
固有周期 (T) = 0.03h
例えば高さ50mのRC造りの場合、固有周期は1秒となります。
固有周期 (T) = 0.02×50 = 1秒
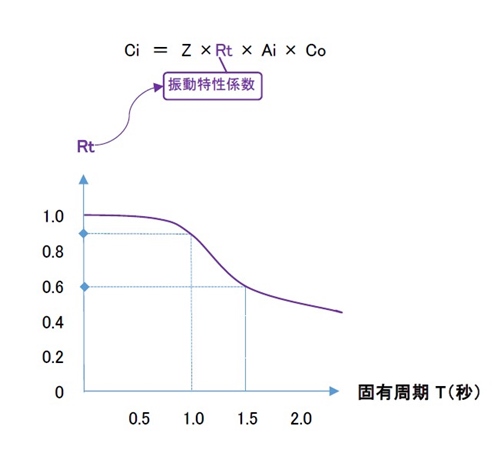
0.02や0.03をかけるので。高さ10mでは0.2秒、0.3秒となって
グラフからRtは1になります。
つまり、低い建物での振動特性係数Rtは、ほぼ関係ないと言えます。
因みにRtは地盤が硬いほど小さくなります。
固有周期が長いほど小さくなります。
高さ方向の分布係数Ai

建物が高いほど、そして軟らかいほど、揺れが大きくなります。
ですから、そうした建物に割り増しの係数を乗じます。
これを高さ方向の分布係数Aiとしています。
Aiは、1階を1として、上に行くほど割り増ししていきます。
つまり1以上の数値を乗じるという事です。
ほとんどの中低層建物はZは1、Rtも1が多く、AiとCoの大きさで
Ciが決まります。
高さによる分布係数Aiは、どうやって求める?
分布係数Aiは、下のグラフから求めます。

縦軸にai(スモールai)、横軸にAi(ラージAi)として、
長さの違う固有周期(T)によって、求めていきます。
1階では、どの周期でも1となります。
グラフからも分かるように、階数が上がるほど、
固有周期が長い(柔らかい)ほど、Aiの割増係数が上がります。
縦軸 ai(スモールai)の求め方
縦軸 ai(スモールai)は下記の式で求めます。
aiのiは階数の事です。
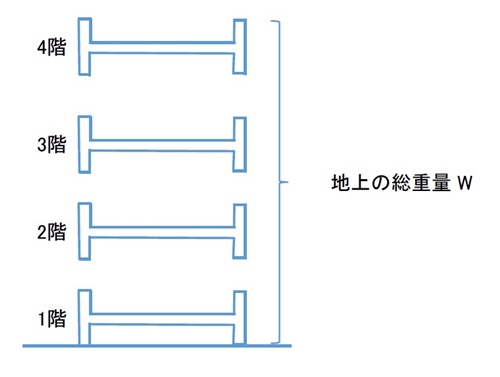
W : 地上から上の総重量
Wi : i階から上の重量
例えば3階のa3は
a3 = w/w3
となります。
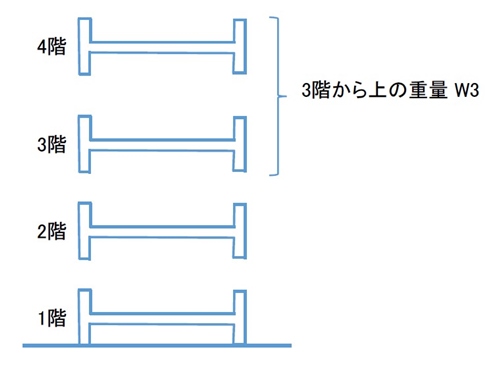
1階が1になる理由
1階の場合は、W とWiは同じになるので1となります。