トップページ ＞ 断面二次モーメントの基本

構造計算 断面二次モーメントとは、断面の曲がりにくさを示す

 

定数です。

 

 

断面の曲がりにくさ

 

 

断面の曲がりにくさは、いくつかの要素で決まります。

 

例えばゴムよりアルミの方が曲がりにくいです。

 

アルミより鉄のほうが曲がりにくいですよね。

 

このように材料によって曲がりにくさが決まります。

 

材料の違いによる曲がりにくさはヤング係数で表されます。

 

 

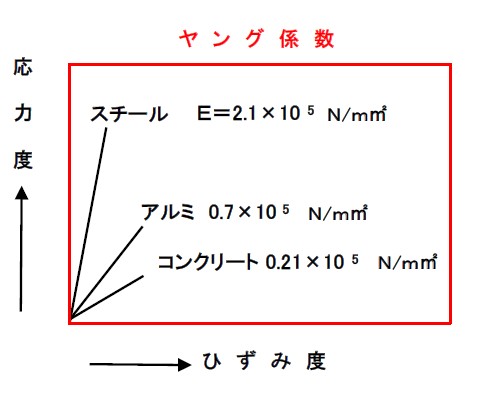
ヤング係数が大きいほど変形しにくい事になります。

 

上の表を見ると鉄はアルミニウムの3倍変形しにくく、

 

コンクリートは鉄の10分の1で変形してしまいます。

 

この表では鉄が一番変形しにくいという事になります。

 

 

ヤング係数だけじゃない変形しにくさ!

 

同じ鉄でも、ただの鉄の棒とＨ型鋼では、

 

Ｈ型鋼のほうが曲がりにくかったり、

 

同じＨ型鋼でも断面積が多きほうが曲がりにくくなる訳です。

 

つまり断面の曲がりにくさ（曲げ剛性）は、

 

ヤング係数（E)と断面2次モーメント(I)の積で求められます。

 

曲げ剛性＝ヤング係数（E)×断面2次モーメント(I)

 

という事になります。

 

 

断面2次モーメント

 

断面2次モーメントは小さな断面積に距離の2乗を掛けたものを

 

寄せ集めたものです。

 

小さな断面積をdaで表します。

 

そして、この場合の距離とは�I軸y軸からの距離です。

 

式で書くとこうなります。

 

 

 

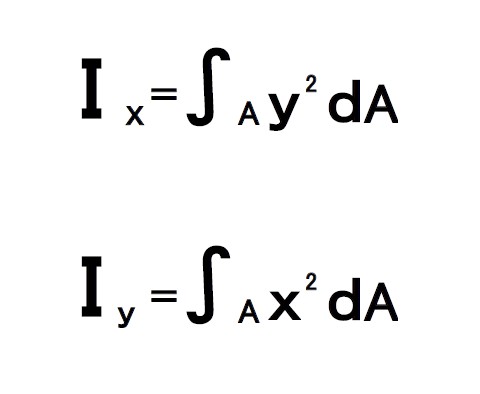
∫は「インテグラル」と読みます。

 

ラテン語の総和を表すSummaの頭文字Sを上下に

 

引き延ばした記号です。

 

式は小さな断面積daに距離の2乗を掛け

 

∫（インテグラル）で寄せ集めたものという意味です。

 

 

この式が、ある�I軸、y軸からの計算式となります。

 

 

 

 

【スポンサーリンク】