構造計算で使うモーメントの基本
モーメントとは、部材を回転する力を言います。
モーメントは回転する矢印で表され、記号は M(エム)
で表されます。
モーメントMの大きさは、力P(ピー)と力までの距離l(エル)で
表されます
M = P × l
モーメントは力(N)と距離(m)の積なので、
単位はN・m や KN・m となります。
モーメントは総和!?
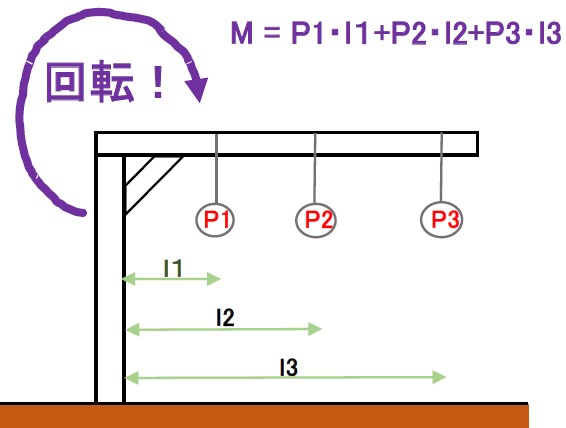
図のようにP1、P2、P3は、横棒を時計周りに
回転させようとしています。
この部材を回転する力こそがモーメントとなる訳です。
この部材のモーメントは力P1、P2、P3と、
その力までの距離を掛けた総和で求められます。
モーメント = P1・l1 + P2・l2 + P3・l3
通常モーメントは時計回りを正、反時計回りを負とします。
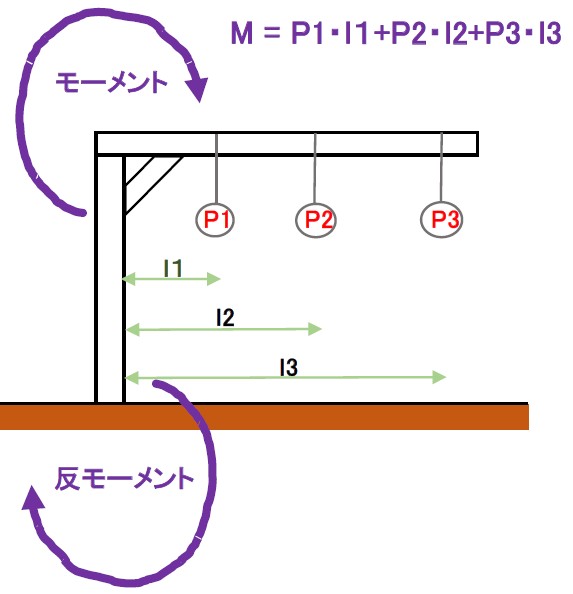
モーメントと反モーメント
モーメントが働いていれば、横棒は回転するはずですが、
この棒は回転せずに静止しています。
これはモーメントと同じ大きさの反モーメントが働いているからです。
モーメントと反モーメントは同じ大きさで反対側に
打ち消しあっているから、この横棒は回転せずに
静止しています。
例題
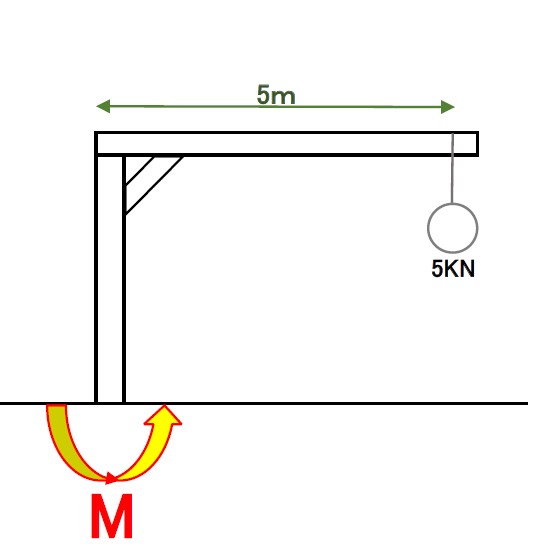
例えば次の図のように水平距離5mのところに
重さ5kNのおもりを付けたときの棒の足元の
曲げモーメントを求めてみましょう。
解答
M = 5kN × 5m = 25KN・m
曲げモーメントMは25KN・mとなります。
【スポンサーリンク】